Cryptol version 2 for version 1 Programmers

Cryptol version 2 makes some changes based on suggestions from the user community and lessons learned by the Cryptol design team. These include syntax changes and some extensions to the type system. Perhaps the the most disruptive change for current Cryptol programmers is that Cryptol version 2 interprets sequences in “big endian” mode, rather than “little endian.”

Current versions of Cryptol version 1 come with a “modernize” command to convert a Cryptol version 1 file to Cryptol version 2. The conversion is not complete, however, and no attempt is made to change the logic of the program that may depend on endianness, so careful human review is still needed. The Cryptol command is

:modernize <infile> <outfile>

Summary of Changes

Here’s a short summary of the syntax changes made in Cryptol version 2:

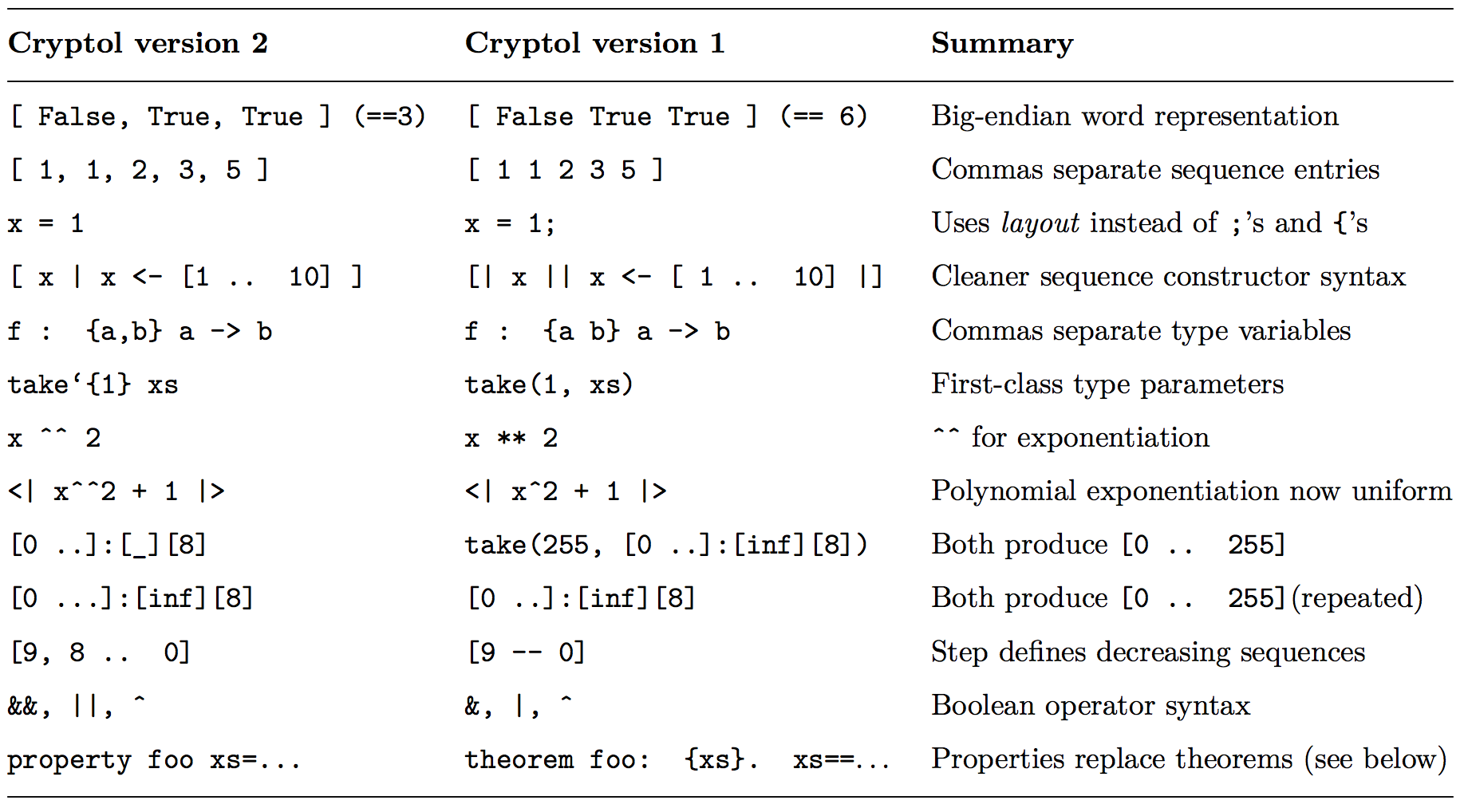
New Features in Cryptol version 2

Sequence Literals

In Cryptol version 1, [0 ..]:[inf][n] constructs an infinitely long list of elements wrapping in n bits. In version 2, the .. syntax creates a finite list that halts before the wrapping would occur.

In version 2, use the ... syntax to construct an infinitely long sequence. One additional change: in version 1 [0 ..] constructs the sequence [0 1 0 1 0 1], and in version 2, [0 ...] constructs the sequence [0, 0, 0, ...]. To produce the list of alternating ones and zeros, specify the width of the elements, as in:

Cryptol> [0 ... ]:[_][1]
[0, 1, 0, 1, 0, ...]

Finally, version 1 used -- for decreasing sequences, but version 2 uses the difference between the first two elements to define the step between elements in the sequence, as in:

Cryptol> [10, 9 .. 0]
[10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
Cryptol> [6, 4 .. 1]
[6, 4, 2]

Layout

Version 1 of Cryptol used curly braces to delimit blocks and semicolons to separate expressions. In version 2, Cryptol has layout-based syntax which uses indentation to delimit blocks and \ to indicate line continuation.

Where in Cryptol version 1 we might write:

caesar : {n} ([8], String n) -> String n;
caesar (s, msg) = [| shift x || x <- msg |] where {
    map     = ['A' .. 'Z'] <<< s;
    shift c = map @ (c - 'A');
};

in version 2 would become:

caesar : {n} ([8], String n) -> String n
caesar (s, msg) = [ shift x | x <- msg ]
    where map     = ['A' .. 'Z'] <<< s
          shift c = map @ (c - 'A')

Module System

The beginning of a Cryptol file can declare that it defines a module:

module Vector where

and can import another module:

import Math

Note that the filename for a module should correspond to the module’s name with a .cry extension. This allows Cryptol to locate imported modules.

Definitions within a module are public by default, but can be hidden from other modules like this:

private internalConstant = 0x55
        anotherInternalConstant = 0x66
externalConstant=0x77

Whenever names might be ambiguous, they can be disambiguated with the :: syntax (using a qualified import using “as”):

import ExternalModule as eModule
...
functionName = ...         // shadows external definition
eModule::functionName xs   // accesses external definition

Multi-way If-Then-Else

Cryptol version 2 supports a “case-statement”-like multi-way branch:

x = if y % 2 == 0 then 1
     | y % 3 == 0 then 2
     | y % 5 == 0 then 3
     else 7

First-class Type Variables

In Cryptol version 1, type variables, such as the first argument to take, were special-cased and could not be written in Cryptol itself, but had to be part of built-in functions. In Cryptol version 2, the named type variables defined in a function’s signature can be referred to when that function is called, either positionally, or by name. This has allowed many of the previously built-in functions to be defined in a Cryptol “prelude” file. You can examine this file by running the Cryptol tool with no argument, and then typing :e. We suggest you not edit this file, however. Here is the definition of take, a previously built-in Cryptol function:

take : {front,back,elem} (fin front) => [front +
                                         back] elem -> [front] elem
take (x # _) = x

Since programmers usually think of take as a one-argument function (the number of elements to take from the head of the list), that argument (front) has been defined first in the signature of take. This lets us call it like this:

take`{3}xs

Which does the same as the Cryptol version 1 call take(3,xs).

Here is the signature for the (still) built-in split:

split : {parts, each, a} (fin each) => [parts *
                                        each]a -> [parts][each]a

and here is how groupBy is defined in terms of split:

groupBy : {each,parts,elem} (fin each) =>
    [parts * each] elem -> [parts][each]elem
groupBy = split`{parts=parts}

We can pass the each argument to groupBy positionally, or by name. These two calls are equivalent:

groupBy`{3}xs
groupBy`{each=3}xs

but we could instead pass the parts argument by name, or positionally as in:

groupBy`{parts=2}
groupBy`{_,2}

The former being preferred whenever it makes the code easier to read.

Finally, you can declare type variables in a function declaration, by typing the function’s arguments, like this:

myWidth (xs:[a]b) = `a

This can help break the Catch-22 situation that sometimes arises when you’re writing a function that needs access to type variables, but you’re not yet sure about the whole function’s type signature.

Type Classes

Cryptol version 2 has introduced type classes to enable type constraints to be more expressive. For example, the type of + in Cryptol version 1 is:

Cryptol> :t +
+ : {a b} ([a]b,[a]b) -> [a]b

and in Cryptol version 2, the type of + is:

Cryptol> :t (+)
+ : {a} (Arith a) => a -> a -> a

This latter type says that the arguments of + must be things that “arithmetic can be performed on”.

The other type class Cryptol version 2 defines is Cmp – the class of things that can be compared to each other:

Cryptol> :t (==)
== : {a} (Cmp a) => a -> a -> Bit

Properties (theorems in version 1)

In version 1, theorems are special syntax attached to function declarations. In version 2, the property keyword can be added to any function that returns a Bit. All of the arguments to a propertyare implicitly universally quantified. So version 1’s

sqDiffThm : ([8], [8]) -> Bit;
theorem sqDiffThm: {x, y}. sqDiff1 (x, y) == sqDiff2 (x, y);

becomes, in version 2:

sqDiffThm : ([8], [8]) -> Bit
property sqDiffThm x y = sqDiff1 (x, y) == sqDiff2 (x, y)

The property keyword is just an annotation. You can apply :check, :sat and :prove to any function that returns Bit.

Current Limitations of :modernize

If you want to translate a significant codebase written in Cryptol version 1 to version 2, the :modernize command can help a lot. However it doesn’t do the whole job for you. This section describes some limitations and suggests effective ways of translating your code.

Syntatic limitations

Currently, :modernize:

• doesn’t add commas to lists of type variables,
• doesn’t automatically translate take(3,xs) to take`{3}xs,
• doesn’t translate ** to ^^,
• doesn’t turn theorem declarations into property’s.

Feature requests have been filed for these limitations.

Converting Endianness

If your code goes back and forth between numeric constants and sequences (as much crypto code does), you have already been affected by version 1’s choice of little endianness, in which the “rightmost” bits of the word are the most significant digits.

Cryptol> [False False True]
0x4

Since humans made the (questionable?) decision to write the most-significant bits first when we write numbers down, many translations of crypto specs involve frequent use of the reverse operator. We have found that Cryptol code looks closer to most specs when it’s in “big endian” mode. This is why version 2 only supports this mode.

The translation between endianness can not be easily mechanized, though, so :modernize doesn’t try to.

As a result, our suggested translation path from version1 to version2 is either to completely rewrite the code based on looking at the original spec (which is likely to produce surprisingly cleaner code), or if that isn’t feasible to first translate the version 1 code to “big endian” mode (use :set +B), then apply :modernize, then finally fix up the source based on the limitations enumerated above. The reason for going this route is that switching endianness within version 1 lets you use the :prove and :check operations to verify the correctness of your logic, then it becomes a simple syntax modernization task. Doing both at once has proven to be very difficult, and leaves you without tool support.